Ghid metodic: Compararea a două fracții

Ghid metodic: Compararea a două fracții cu același numărător sau numitor la clasa a IV-a

Pe parcursul învățământului primar, procesul de învățare a matematicii implică înțelegerea conceptelor de bază precum fracțiile.

O etapă crucială în acest proces este compararea a două fracții, unde elevii încep să exploreze conceptul de ordine în mulțimea fracțiilor.  Problema comparării a două fracţii apare imediat după problema egalităţii.

La clasa a IV -a, sunt abordate două situaţii în compararea fracţiilor:

1)  fracţiile au acelaşi numitor;

2)  fracţiile au acelaşi numărător.

Situația 1: Fracțiile cu același numitor

Când fracțiile au același numitor, elevii pot înțelege intuitiv că fracția cu numărătorul mai mic reprezintă o cantitate mai mică din întreg deoarece se „iau mai puţine unităţi fracţionare”.

De exemplu, în cazul fracțiilor 3/8 și 5/8, deoarece ambele fracții împart întregul în 8 părți egale, fracția 3/8 este mai mică decât 5/8, deoarece reprezintă mai puține părți din întreg. În exemplul cu pizza, dacă alegem 3 felii, avem o cantitate mai mică decât dacă alegem 5 felii.

Regula numărul 1 : Fracția cu numărătorul mai mic reprezintă o cantitate mai mică din întreg.

Regula numărul 2 : Ca să putem compara două fracții, acestea trebuie să fie părți ale aceluiași întreg sau părți din întregi identici.

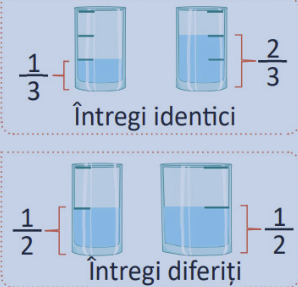
Situația 2: Fracțiile cu același numărător

Atunci când fracțiile au același numărător, folosind exemple concrete, arătăm că, împărțind întregul în mai multe părți egale, fiecare parte devine mai mică.

Exemple concrete:

1) tăiem un măr în două părți egale, respectiv în patru părți egale. Elevii sunt întrebați care este partea pe care o aleg?

2) procedăm în același mod cu o mulțime de 12 bomboane pe care le impărțim în 3 părți, respectiv 4 părți. Care parte este mai mare?

În acest fel, elevii pot realiza că 1 /2 > 1 /3 > 1 /4 > . . . , adică, dintre două unităţi fracţionare diferite este mai mare cea cu numitorul mai mic.

Astfel, pentru elevi devine mai ușor și intuitiv să ordoneze descrescător sau crescător mai multe unităţi fracţionare diferite. După asimilarea faptului că 1 /2 > 1 /3 , se deduce imediat că 1 /3 < 1 /2

Regula numărul 1: Dintre două unităţi fracţionare este mai mică cea care are numitorul mai mare.

Regula numărul 2: Ca să putem compara două fracții, acestea trebuie să fie părți ale aceluiași întreg sau părți din întregi identici.

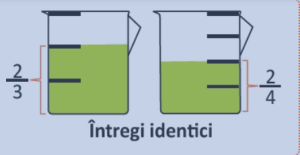
Cunoscând faptul că o pătrime reprezintă mai mult decât o cincime (din acelaşi întreg sau din doi întregi egali), elevii intuiesc cu uşurinţă că dacă se iau câte 2 asemenea părţi, 3 pătrimi înseamnă mai mult decât 3 cincimi.

După mai multe exemple concrete, se poate generaliza : dintre două fracţii cu acelaşi numărător este mai mare cea cu numitorul mai mic.

Sarcini de lucru recomandate:

• Stabilirea celei mai mari fracții dintr-un set;
• Compararea și ordonarea fracțiilor cu același numărător sau numitor;
• Ordonarea fracțiilor crescător sau descrescător.

Concluzie

Compararea a două fracții reprezintă o etapă esențială în înțelegerea conceptelor de bază ale fracțiilor în cadrul învățământului primar.

Prin utilizarea acestui ghid metodic și a unor exemple concrete și activități practice, profesorii pot facilita înțelegerea acestui concept important în matematică.